Дерево решений является разновидностью дерева событий. В дереве событий рабочие состояния системы не рассматриваются, так что сумма вероятностей всех событий не равна единице. В дереве решений все возможные состояния системы необходимо выразить через состояния элементов. Таким образом, все состояния системы взаимно увязаны, и их вероятность в сумме должна равняться единице. Деревья решений могут использоваться, если отказы всех элементов независимы или имеются элементы с несколькими возможными состояниями, а также есть односторонние зависимости. Они не могут использоваться при наличии двусторонних зависимостей и не обеспечивают логического анализа при выборе начальных событий.
ПРИМЕР. На рис. 6.10.1 показана система последовательно соединенных элементов, которая включает насос и клапан, имеющие соответственно вероятности безотказной работы 0,98 и 0,95, а также приведено дерево решений для этой системы. Следует отметить, что согласно принятому правилу верхняя ветвь соответствует желательному режиму работы системы, а нижняя - нежелательному. Дерево решений читается слева направо.
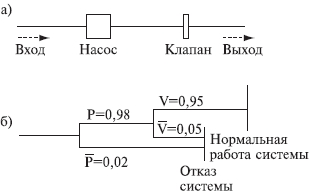
Рис. 6.10.1. Принципиальная схема (а) и дерево решений (б) для двухэлементной системы
Если насос не работает, система отказывает независимо от состояния клапана. Если насос работает, с помощью второй узловой точки изучается вопрос, работает ли клапан.
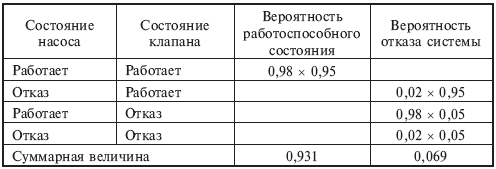
Вероятность безотказной работы системы: 0,98(0,95=0,931. Вероятность отказа: 0,98(0,05+0,02=0,069, а суммарная вероятность двух состояний системы равна единице.
Этот результат можно получить другим способом с помощью таблицы решения, которая для насоса и клапана имеет вид:

 3046
3046  ~1 мин
~1 мин









